Παιχνίδια!
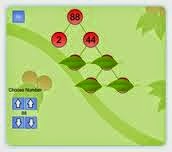
Με τα βελάκια σχηματίζεις τον αριθμό που θα αναλύσεις. Μετά πατάς το Go .
.
 .
.
Όταν εμφανιστεί ο αριθμός, κάνε κλικ στα φύλλα, για να δεις την ανάλυση του αριθμού.
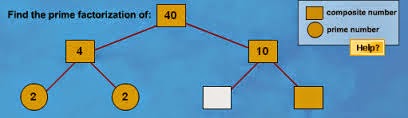
Γράφεις μέσα στα κουτάκια την ανάλυση του αριθμού που βλέπεις στην κορυφή και πατάς  . Συνεχίζεις μέχρι την ολοκλήρωση της.
. Συνεχίζεις μέχρι την ολοκλήρωση της.
Γράφεις στο λευκό κουτάκι έναν παράγοντα του αριθμού και πατάς Enter.
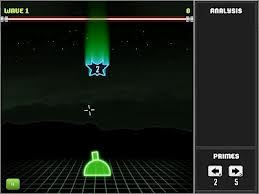
Πυροβόλησε τους αριθμούς με το κανόνι.
Με το ποντίκι σημαδεύεις τους αριθμούς και με τα βελάκια του πληκτρολογίου (δεξιό και αριστερό) ρίχνεις τους πρώτους αριθμούς που φαίνονται κάτω δεξιά στην οθόνη σου.
Πρέπει να πυροβολείς κάθε αριθμό με έναν διαιρέτη του , ώσπου να γίνει 1. Π.χ. Τον αριθμό 25 τον πυροβολείς με το 5 και γίνεται 5 (25:5) , ύστερα ξανά με το 5 και γίνεται 1 (5:5).
Επανάληψη