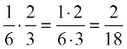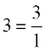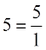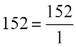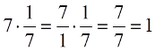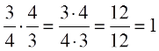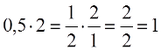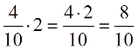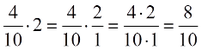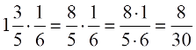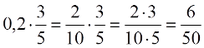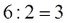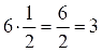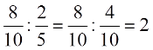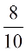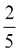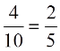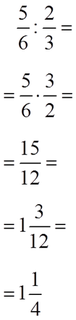Όταν ο άγνωστος είναι παράγοντας γινομένου, για να λύσουμε την εξίσωση διαιρούμε το γινόμενο με τον άλλο παράγοντα.
Η ισορροπία της εξίσωσης διατηρείται, αν διαιρέσουμε και τα δυο μέρη με τον ίδιο αριθμό.
ΤΙ ΠΡΕΠΕΙ ΝΑ ΘΥΜΑΜΑΙ:
- Όταν σε μια εξίσωση ψάχνω κάποιον από τους δυο παράγοντες του πολλαπλασιασμού, κάνω διαίρεση.
- Διαιρέτη βάζω πάντα τον αριθμό που είναι μαζί με το X (συντελεστή του αγνώστου) και διαιρετέο το γινόμενο.
- Για να κάνω διαίρεση με κλάσματα, αντιστρέφω τους όρους του β΄ κλάσματος και αντί για διαίρεση κάνω πολλαπλασιασμό.
- Για να κάνω διαίρεση με μεικτούς, πρέπει να τους μετατρέψω όλους σε κλάσματα.
- Δεν μπορώ να κάνω διαίρεση αν ο διαιρέτης είναι δεκαδικός. Πρέπει να τον κάνω ακέραιο πολλαπλασιάζοντάς τον με το 10, 100, 1000, κ.τ.λ. ανάλογα με τα δεκαδικά του ψηφία. Το ίδιο πρέπει να κάνω και με τον διαιρετέο.
Πηγή : έκτη και ... τελευταία
Είτε ο άγνωστος είναι στον α΄είτε στον β΄παράγοντα, με τον ίδιο τρόπο τον βρίσκουμε!
Πρόβλημα α:
Η ΣΤ' τάξη έφτιαξε για το χριστουγεννιάτικο παζάρι κουραμπιέδες και τους πουλούσε προς 8,5 Ευρώ το κιλό. Πόσα κιλά κουραμπιέδες πούλησε αν εισέπραξε 204 Ευρώ; ( χ . 8,5 = 204)
Πρόβλημα β :
Η ΣΤ' τάξη έφτιαξε για το χριστουγεννιάτικο παζάρι 24 κιλά κουραμπιέδες και εισέπραξε 204 Ευρώ. Πόσο κόστιζε το κιλό; ( 24 . χ = 204)
Σκέψου ότι έχεις ένα πολλαπλασιασμό απλό . Π. χ. 3 . 8 = 24
Οι διαιρέσεις που προκύπτουν από τον παραπάνω πολλαπλασιασμό είναι: 24 : 3 = 8 και 24 : 8 = 3
Άρα καταλαβαίνεις ότι για να βρούμε τον άγνωστο χ που είναι παράγοντας γινομένου αρκεί να διαιρέσουμε το γινόμενο με τον άλλο γνωστό παράγοντα.
Γράφουμε τις εξισώσεις:
Πρόβλημα α :( χ . 8,5 = 204 ή χ = 204 : 8,5 ή χ = 24)
Πρόβλημα β : ( 24 . χ = 204 ή χ = 204 : 24 ή χ = 8,5)
Πηγή : Εγκύκλιος παιδεία
ΕΞΑΣΚΗΣΗ 1 (κλικ)
ΕΞΑΣΚΗΣΗ 2 (κλικ στο σύνδεσμο)

ΕΞΑΣΚΗΣΗ 3 (κλικ στο σύνδεσμο)